https://www.acmicpc.net/problem/2293
아래 내용 이해한다면 모두 이해한 것임.
구성이 같더라도 순서가 다른것을 모두 다르게 취급하는 경우 (countSum문제)
==>>dp for문에서 아이템의 항목들을 내부반복문으로 사용
구성이 같더라도 순서가 다른것을 모두 같게 취급하는 경우(일반적이지 않은 경우로 직관적으로 이해되진 않음) (동전1 문제)
==>>dp for문에서 아이템의 항목들을 외부반복문으로 사용(아이템의 항목들이 외부반복문으로 사용되므로 2차원 테이블로는 만들수 없음. 다만 이해를 돕기 위해 2차원 테이블을 그림)
dp[j]+=dp[j-i] 의 의미: dp[j] => 새로운 수를 사용하지 않은 이전의 수만 사용한 기존의 경우. dp[j-i] =>새로운수와 기존의 수를 모두 사용하여 이전의 목표치를 이룬 경우의 수(재밌는 것이 새로운 목표치 j에서 새로운 수 i를 빼준것을 새로운 목표치j에 더해주고 있으니 암묵적으로 i를 더해주면 j가 된다는 사실을 나타내고 있다. 이말이 이 글을 다시 볼때도 선뜻 이해 되었으면 좋겠다).
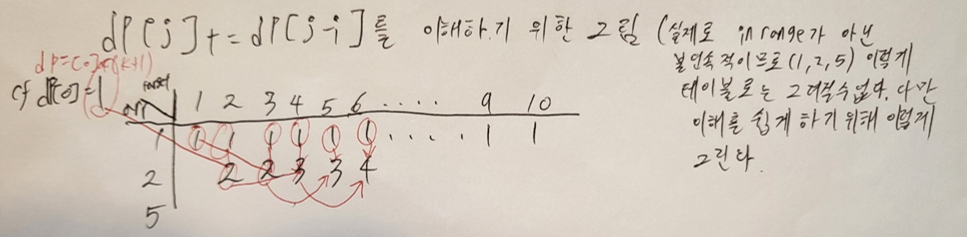
이 문제 해법을 이해하는데 참 많은 시간이 걸렸다. 우선 다른 연관된 문제와 함께 생각해 보면 이렇다.
기본적으로 CanSum 문제는 되는지 안되는지만 파악하기 때문에 비교적 쉽다.
from sys import stdin
import sys
def canSum(arr, target):
check=[False]*(target+1)
check[0]=True
for i in range(0, target):
if(check[i]):
for j in arr:
if(i+j<=target):
check[i+j]=True
if(check[target]):
print("true")
else:
print("false")
def main():
n=int(sys.stdin.readline())
for _ in range(n):
target,num=map(int, input().split())
arr=list(map(int, input().split()))
canSum(arr, target)
main()여기서 한 걸음더 나아가서 CountSum인데, 이문제가 countSum과 다른점은 순서만 다르다면 같은 걸로 취급한다는 것이다(CountSum은 순서가 다르면 다른것으로 취급).
내가 학교알고리즘(School Algo)10장에서 충분히 점화식의 의미를 파악하지 못한 것을 여기서 분석해 보면 이렇다. 우선 코드는 아래와 같다.
def countSum(arr, k):
dp=[0]*(k+1)
dp[0]=1
for i in range(k+1):
if(dp[i]!=0):
for j in arr:
if(i+j<=k):
dp[i+j]+=dp[i]
print(dp[k])맨처음 기저사례를 두기위해 dp[0]=1(주워진 수로 0을 만드는 방법의 경우의 수는 아무것도 포함하지 않는 경우로 1로 둠) 로 두고 i+j라는 수가 k를 넘지만 않는다면 dp[i+j]= dp[i+j]+dp[i] 라는 점화식을 수행해 준다. 이 점화식의 의미는 기존의 dp[i+j]를 가져오고 dp[i]에 j를 살포시 얹은것을 더해 준다는 것이다. 이게 무슨 말일까?
dp[i]를 만족하는 경우와 거기다 j만 하나 얹은 것의 경우의 수는 같다. 즉 dp[i+j]=dp[i]로 취급하고 거기다 j만 의미상 얹어준다는 것이다(이는 아래의 동전 문제를 풀면서 더 구체적으로 그 의미를 알수 있다.).

마지막으로 최종 문제인 동전문제이다. 이 문제가 CountSum과 다른점은 순서가 바뀌어도 같은 것으로 취급한다는 것에 있다.
#일반적인 countSum, canSum이 문제가 아니다. 각각의 요소를 중복해서 사용할
#수 있다. 반면 일반적인 Subset Sum문제는 중복이 허용되지 않는다.
#countSum문제와 다른점은 countSum에서는 7을 만들때 3,4와 4,3을 서로 다른 경우로
#카운트하지만 이 문제에서는 같은 경우이다.
from sys import stdin
def solution(arr, k):
dp=[0]*(k+1)
dp[0]=1
for i in arr:
for j in range(i, k+1):
dp[j]+=dp[j-i]
print(dp[k])
def main():
n,k=map(int, stdin.readline().split())
arr=list()
for i in range(n):
arr.append(int(stdin.readline().strip()))
solution(arr, k)
main()그리고, 흥미로운 점은 내부반복문과 외부반복문을 서로 바꾸어 주고 약간의 수정만 해주면 순서에 상관없이 카운팅할지, 순서와 관계지어 카운팅할지 구분 된다는 것이다.
(24.2.2) 지금에 와서 드는 생각이지만 그냥 dp[j]+=dp[j-i]; 라는 식 자체에 의미를 두는 식으로 기억하는것도 괜찮은거 같다. +의 의미는 누적을 의미한다. 즉, arr=[1,2,5]일때 처음으로 1의 경우를 모두 해보고 그다음 2의 경우를 넣어서 해볼때 이전의 1의 경우일때를 모두 가져오는 것이다. 그것이 +의 의미이다. j-i에서 -의 의미는 해당수를 살포시 얹는 것을 의미한다. 마지막으로 위의 식이 무언가를 중복허용하고 순서는무시되는(구성이 같으면 순서가 다르더라도 뭉뚱그려 하나로 취급)조건에서 사용되는 점화식이라고 그냥 기억하는것도 좋을 것 같다. (아래 블로그 글은 내가한 이 생각을 좀더 자세히 풀어쓴 것이다)
출처: https://seongonion.tistory.com/108
시간제한이 0.5초로 DP를 이용해 아주 빠르게 풀어야하는 문제이다.
테스트 케이스를 예제로 점화식을 세워보자.
우선, 1원을 가지고 1 ~ 10원까지 만드는 경우의 수는 모두 1이다.
그 다음으로, 1원과 2원을 가지고 1 ~ 10원까지를 만드는 경우의 수를 생각해보자.
2원으론 1원을 만들 수 없으니, 1원은 오직 1원으로만 만들 수 있으므로 경우의 수는 그대로 1이다.
2원을 만들기 위해선 기존에 1원으로만 만들었던 (1원, 1원)에 더해 새로 추가된 동전을 사용하는 경우(2원)가 추가되므로 2개가 된다.
3원을 만드는 경우를 보자.
우선, dp테이블에 3원을 1원으로 만드는 경우의 수는 이미 업데이트 되어있다.
2원이 추가됨으로써 만들어질 수 있는 경우의 수만 더해주면 되는 것이다.
이해하기 쉽게 직접 써보면, (1원, 1원, 1원)에 (1원, 2원)으로, 총 2가지 경우의 수가 존재하고, 2원이 추가되며 새로 만들어진 경우의 수는 (1원, 2원) 조합이다.
자, 여기서 3은 1과 2를 더한 수임을 주목하자.
그렇다면 3원을 만들 수 있는 경우의 수는 1원을 만들수 있는 경우에 2원을 그저 추가해준 것으로, 경우의 수 자체는 동일하다.
즉, dp[3] = dp[1]인 것이다.
와닿지 않는다면 4원을 만드는 경우도 고려해보자.
4원은 (1원, 1원, 1원, 1원), (1원, 1원, 2원), (2원, 2원) 이렇게 총 3개의 조합으로 만들 수 있다.
4는 2와 2를 더한 수이다.
즉, 4원을 만들 수 있는 경우의 수는 2원을 만들 수 있는 경우에 2원 하나를 추가해준 것으로, 이 역시 경우의 수가 동일하다.
즉, dp[4] = dp[2]이다.
즉, dp[2]인 경우의 수 (1원, 1원)과 (2원) 조합에 각각 2원을 추가해주어 (1원, 1원, 2원), (2원, 2원)이 되고, 처음에 1원으로만 4원을 만들었던 경우의 수 한 가지 (1원, 1원, 1원, 1원)을 더하면 총 3가지의 경우의 수가 나온다.
이를 점화식으로 표현하면, dp[i] += dp[i - coin]이 된다.
DP문제를 잘 해결하기 위해선 2가지가 중요한 것 같다.
첫 번째는 점화식을 세우는 것이고, 두 번째는 dp[i]에 도달하기 이전인 0 ~ i - 1 까지는 최적의 값이 저장되었다고 확신하는 것이다.
구현 문제처럼 즉각적으로 답이 보이는 게 아니기 때문에, 자꾸 예외처리에 신경을 쓰게 되고 그러다보면 정확한 점화식을 세우는 데 집중하지 못하게 된다.
DP는 점화식으로 푸는 문제임을 명심하자.
'알고리즘 > DP(Dynamic programming, 동적프로그래밍)' 카테고리의 다른 글
| 백준(BOJ) 1010번 다리놓기 (1) | 2023.11.09 |
|---|---|
| 백준(BOJ) 9095 : 1, 2, 3 더하기 (countSum과 같은 문제) (0) | 2023.08.18 |
| [백준] 11066번: 파일 합치기 (0) | 2023.05.20 |
| [백준] 9251번 : LCS(Longest Common Subsequence) (0) | 2023.05.19 |
| 배낭채우기 문제 (0) | 2023.02.28 |

