0,1 배낭채우기 문제
출처:https://gsmesie692.tistory.com/113
내정리: 중요한 것은 Greedy이든 Dynamic Programming이든 같은 종류의 문제(최댓값을 구하라, 최소값을 구하라등)에 적용될 수 있는 해결책들이라는 것이다. 다만 탐욕적 방법이 안될때 동적 기법이 사용될 수 있다는 것이 차이점이다. 따라서 어떤 문제를 볼때 어느 하나만 생각하는 것은 옳지 않다. 모든 기법을 생각할 수 있는 것이 자연스러운 것이다.
도둑이 보석가게에 배낭을 메고 침입했다.
배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 찢어질 것이다.
각 보석들의 무게와 가격은 알고 있다.
배낭이 찢어지지 않는 선에서 가격 합이 최대가 되도록 보석을 담는 방법은?
흔히 알고리즘을 배울 때 자주 등장하는 문제 중 하나인 배낭 채우기 문제 (Knapsack Problem) 이다. 그 중에서도 보석을 자를 수 있다고 가정하는 Fractional Knapsack 문제와 자를 수 없다고 가정하는 0-1 Knapsack 문제가 있는데, 전자보다는 후자가 주로 다루어진다.
0-1 Knapsack 문제는 다이나믹 프로그래밍 (Dynamic Programming: DP) 이라는 방법을 쓰는 기본적인 문제로 알려져 있다. 알고리즘 문제를 푸는 방법론들에 대해서 아직 잘 모르는 상태에서 이 문제를 보면 딱 생각나는 방법은 두 가지 정도가 있을 것이다.
1) 모든 경우의 수를 넣어본다 (Brute-Force)
n개의 보석이 있다고 치면, n개 보석으로 만들 수 있는 가능한 부분집합 (power set) 의 수는 2^n개이다. 최악의 경우에 2^n번까지 봐야 하는, 즉 O(2^n) 의 알고리즘은 너무 느리다.
2) 가격이 높은 보석, 혹은 (가격/무게) 의 값이 제일 높은 보석부터 먼저 골라서 넣는다 (Greedy)
아래의 그림을 보자. 가격이 제일 높은 보석을 먼저 고르는 방법을 쓴다고 하면, 오른쪽 아래에 있는 빨간 보석을 먼저 고르고 그 다음 왼쪽에 있는 노란 보석을 고를 것이다. 그러면 10kg가 차고 가격의 합은 $16이 된다.
그렇지만 그림을 잘 보면서 다른 방법을 찾아보면, 왼쪽 보석 3개를 넣으면 10kg/$17이 된다는 걸 쉽게 알 수 있고, 1/2/3/4kg짜리를 하나씩 조합해서 넣으면 $19까지도 나온다. 즉 이 방법은 최적의 답을 보장하지 못한다.
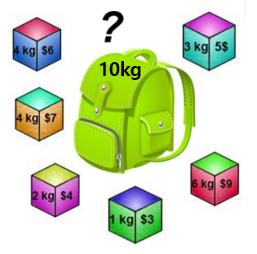
단순히 가격만 보지 말고, '무게당 가격' 을 계산해서 제일 높은 것부터 넣으면 되지 않겠느냐고 생각할 수 있다. 실제로 위 그림의 예시에서는 그렇게 하면 최적의 답이 나오긴 한다. 하지만 언제나 그렇지는 않다. 다른 예시를 보자.
W=30kg
보석1: 5kg/$5 -- kg당 $1
보석2: 10kg/$6 -- kg당 $0.6
보석3: 20kg/$14 -- kg당 $0.7
이 경우에 '무게당 가격' 순으로 보석을 넣으면 보석1, 보석3이 들어가며 가격의 합은 $19이다. 그런데 배낭 무게가 5kg가 남는다. 보석2를 넣을 수는 없으므로 5kg는 그냥 쓸데없이 남는 공간이다. 보석2, 보석3을 넣으면 30kg가 꽉 차고 가격의 합이 $20이다. 도둑 입장에서 도망갈 때 배낭이 좀 더 무거울 수 있겠지만 어쨌든 문제의 조건은 배낭이 안 터지는 한도 내에서 가격 합을 최대화하는 것이므로 보석2, 3을 가져가는 것이 정답이다.
이처럼 특정한 기준을 정해놓고 그 기준의 값이 가장 높은 순으로 집는 걸 Greedy 알고리즘이라 하는데 0-1 배낭 채우기 문제는 Greedy한 방법으로는 풀 수 없는 문제이다.
참고: Fractional Knapsack 문제는 Greedy로 풀 수 있다. 위 예시에서 보석2를 반으로 잘라서 남은 5kg짜리 공간에 넣으면 그게 최적의 답이 된다
그래서 DP라는게 등장한다. DP는 큰 문제를 작은 문제로 쪼개서 해결한다 (Devide-and-Conquer) 라는 원리에 기반을 두고 있으며, 이전에 계산해둔 값을 메모리 (배열 등) 에 저장해서 반복 작업을 줄이는 기법 (Memoization) 이 핵심이다. 뭔 소리냐면 아래의 피보나치 수열을 계산하는 함수의 예시를 보자.
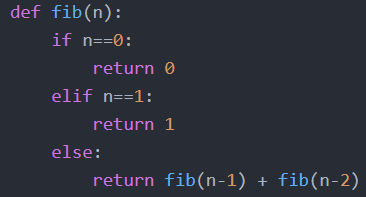
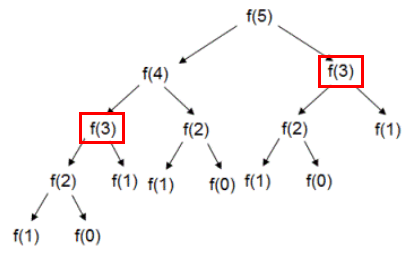
왼쪽은 피보나치 수열을 계산하는 파이썬 함수이다. 피보나치 수열을 구하는 문제는 재귀함수를 이용하는 대표적인 문제로 잘 알려져 있다. 여기서도 재귀를 사용해서 가장 기본적인 방법으로 구현했다.
fib(5) 를 호출했다고 생각해보면 오른쪽 그림과 같이 재귀함수가 호출된다. 근데 빨간색으로 표시한 부분을 보면 왼쪽에서 이미 f(3) 을 한번 호출했는데, 오른쪽에서도 또 호출하고 있다. DP의 아이디어는 계산하는 값들을 어디다 저장해뒀다가, 저런 식으로 중복되는 계산이 나오면 저장해뒀던 값을 갖다 쓰자는 것이다. 그림에서 f(3) 의 값이 저장되어 있는 상태에서 f(3) 이 호출되면 그 값을 갖다 쓰도록 만들면, 오른쪽 트리의 f(3) 아래쪽 부분은 계산할 필요가 없게 된다.
아래는 DP를 적용한 피보나치 함수와 fib(40) 을 실행했을 때의 실행 시간 차이를 보여주는 것이다. 'memo' 라는 dict를 만드는데 메모리 공간을 소비하는 대신, 속도가 비약적으로 빨라지는 것을 알 수 있다.
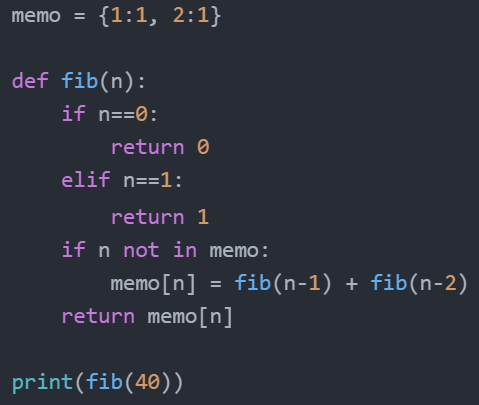
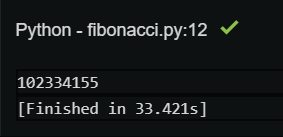
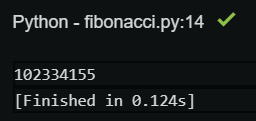
이런 방법이 대체 어디가 다이나믹하냐 하면... 사실 다이나믹이라는 단어는 별 의미 없다. DP의 창시자에 따르면 다이나믹 프로그래밍이라는 이름은 연구비를 따와야 하는데 뭔가 있어보이는 이름이 필요해서 적당히 붙인 이름이라고 한다. (...) 대학원 다녀본 입장에서 공감된다
여튼 이 방법, DP를 0-1 배낭 채우기 문제를 푸는데 적용해보자. 어떤 문제를 DP로 풀기 위해서는 '최적의 원리' (Principle of Optimality) 가 성립하는지를 확인해야 하는데, 최적의 원리란 다음과 같다.
"최적해의 부분해가 또다시 그것의 부분 문제의 최적해가 될때 최적의 원리가 성립한다."
즉, 작은것을 이용해 큰것을 구성할 수 있어야지만 다이나믹 프로그래밍이 가능한 것이다. 역으로 생각하면 DP를 이용한 문제는 모두 그 해답이 작은것과 큰 것이 연관된다는 것이다.
이 문제에서 이 원리가 성립할까? 집합 A를 n개의 보석들 중에 최적으로 고른 부분집합이라고 가정하자.
- 집합 A가 n번째 보석을 포함하고 있지 않다면, A는 n번째 보석을 뺀 나머지 n-1개의 보석들 중에서 최적으로 고른 부분집합과 같다.
- 집합 A가 n번째 보석을 포함하고 있다면, A에 속한 보석들의 총 가격은 n-1개의 보석들 중에서 최적으로 고른 가격의 합에다가 보석 n의 가격을 더한 것과 같다. (단, n번째 보석을 넣었을 때 배낭이 터지지 않아야 한다)
지금 쓴 얘기를 점화식으로 풀어보면 아래와 같다.
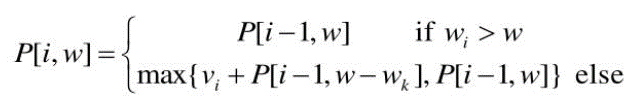
P[i, w] 란 i개의 보석이 있고 배낭의 무게 한도가 w일 때 최적의 이익을 의미한다(여기서 주의할 것은 w는 문제에서 주워진 정해진, 배낭이 감당할 수 있는 무게가 아님! w역시 변하는 부분사례의 값들중 하나임). 식을 좀 문장으로 풀어보면 이렇다.
- i번째 보석이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 보석을 뺀 i-1개의 보석들을 가지고 구한 전 단계의 최적값을 그대로 가져온다
- 그렇지 않은 경우, i번째 보석을 위해 i번째 보석만큼의 무게를 비웠을 때의 최적값에 i번째 보석의 가격을 더한 값 OR i-1개의 보석들을 가지고 구한 전 단계의 최적값 중 큰 것을 선택한다
P라는 2차원 리스트를 채워나가면서, 필요한 경우 "앞에서 계산했던 다른 칸의 값을 이용해서" 다음 칸의 값을 계산한다. 그래서 이게 DP 문제인 것이다.
(최적해(P[i,w])의 부분해(P[i-1, w-wk], P[i-1, w])가 또 다시 그것의 부분문제(i-1, w-wk, w이런 것들이 일종의 부분문제이다)의 최적해(P[i-1, w-wk], P[i-1, w]) 로 구성되고 있다. 따라서 0-1배낭문제는 DP를 이용하여 해결할 수 있는 문제가 된다.)
아래 대문자 W 는 오타임. 소문자 w로 변경해야 함.
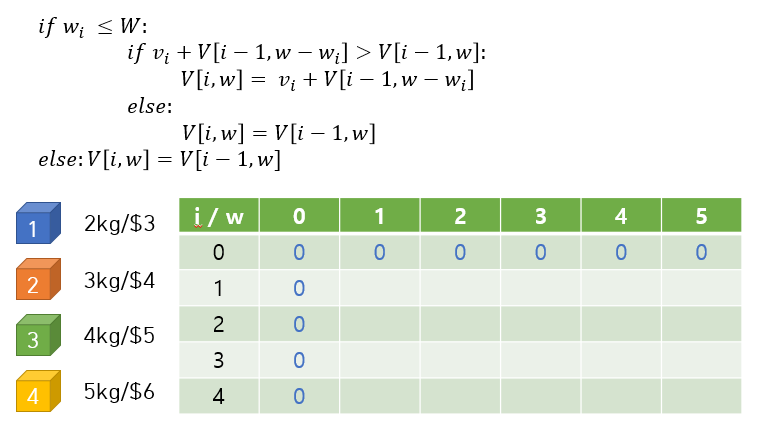
DP를 위한 2차원 리스트가 만들어지는 과정을 한번 보자 (위에서는 P였는데 여기서는 V로 썼다).
일단 i가 0인 경우는 넣을 보석이 없는 것이므로 다 0이고, w가 0인 경우는 배낭이 없는 것이므로 다 0이다. 그러니까 첫번째 행이랑 첫번째 열은 다 0으로 채워넣고 시작한다.
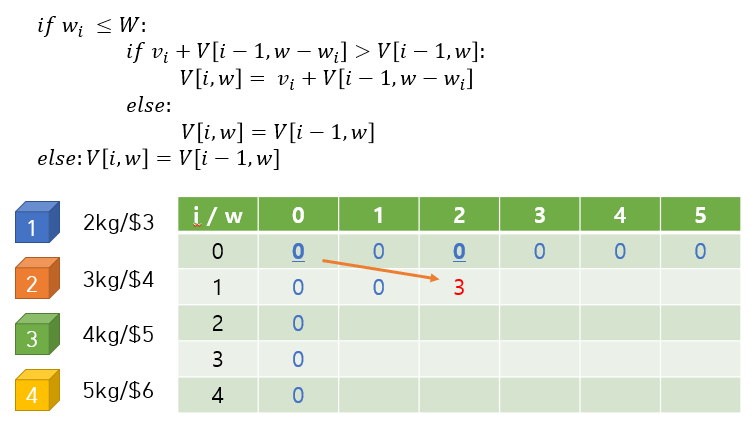
i=1인 경우부터 한칸씩 보자. (i, w)가 (1, 1) 인 경우에는 w=1짜리 배낭으로는 아무 보석도 넣을 수 없으므로 0이다. 그 다음 칸, (1, 2) 인 경우에는 이제 1번 보석을 넣을 수 있으니까 V[1, 2] = 3이 된다. 직관적으로는 이렇고, 위의 식을 통해서 보면 '1번 보석의 가치 + V[0, 0]' 의 값과 V[0, 2] 의 값을 비교해서 더 큰 쪽을 가져가게 되는데, 1번 보석의 가치는 3이고 V[0, 0] 과 V[0, 2] 는 둘 다 0이므로 전자를 선택하게 된다.
현재 i=1이므로 1번 보석을 넣고 나면 더 이상 넣을 게 없으니 오른쪽의 남은 칸들도 다 3일 것이다.
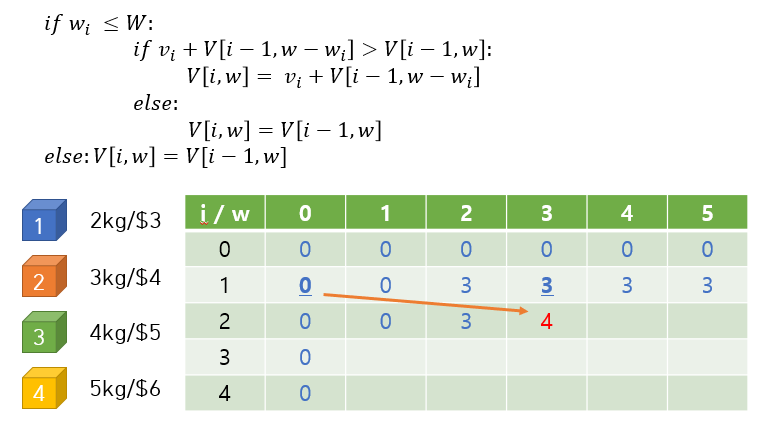
i=2인 경우를 보면, w=2일때는 현재 보고있는 2번 보석 (3kg) 을 넣을 수 없으므로 바로 윗칸의 3을 가져온다 (1번 보석을 넣는다는 뜻. 입력사례의 최적해가 입력사례를 분할한 부분사례의 최적해로 구성되고 있으므로 최적의 원리가 성립하게 된다). w=3이 되면 2번 보석을 넣을 수 있게 되는데, 1번 보석을 넣었을 때 (바로 윗칸) 랑 2번 보석을 넣을만큼의 공간을 확보하고 2번 보석을 넣었을 때 (즉, 2번 보석의 가치 + V[1, 0]) 를 비교해서 더 가치가 높은 쪽을 선택한다. 그래서 4가 들어간다.

(i, w) 가 (2, 5) 인 경우에는 1번 보석과 2번 보석을 둘 다 넣을 수 있다. 이미 3이 들어있는 (1, 2) 에서 최적값을 가져온다는 것이 1번 보석을 빼지 않고도 2번 보석을 넣을 수 있음을 의미한다. 즉 1번 보석을 넣었던 칸의 최적값 (3) + 2번 보석의 가격 해서 7이 들어간다.
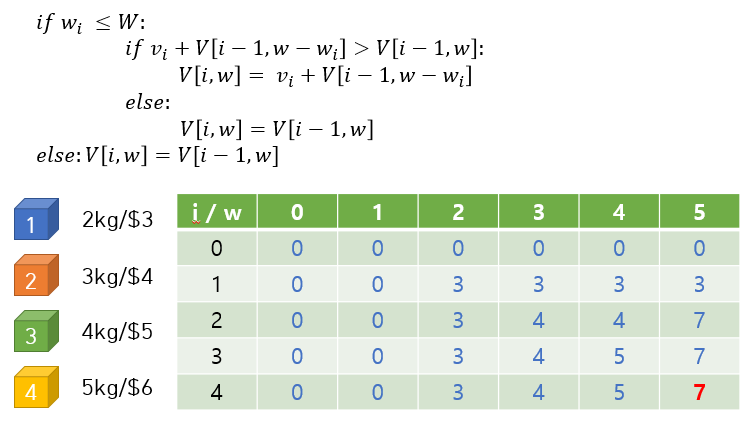
이런 식으로 나머지 칸들도 계산해보면 마지막 칸에는 결국 7이 들어가고, 이 마지막 칸의 값이 최종적인 답 (최적의 총 가격) 이 된다.
아래는 이를 파이썬 함수로 구현한 것이다. DP를 위한 2차원 리스트를 만든 다음, 0번째 행/열을 0으로 세팅하고 나면 나머지는 위의 점화식을 그대로 프로그램으로 옮기면 된다. 위에선 P, V였던게 여기선 또 K인데 신경쓰지 말자
def knapsack(W, wt, val, n): # W: 배낭의 무게한도, wt: 각 보석의 무게, val: 각 보석의 가격, n: 보석의 수
K = [[0 for x in range(W+1)] for x in range(n+1)] # DP를 위한 2차원 리스트 초기화
for i in range(n+1):
for w in range(W+1): # 각 칸을 돌면서
if i==0 or w==0: # 0번째 행/열은 0으로 세팅
K[i][w] = 0
elif wt[i-1] <= w: # 점화식을 그대로 프로그램으로
K[i][w] = max(val[i-1]+K[i-1][w-wt[i-1]], K[i-1][w]) # max 함수 사용하여 큰 것 선택
else:
K[i][w] = K[i-1][w]
return K[n][W]
백준 온라인 저지의 12865번 문제가 정확히 이 0-1 배낭 채우기 문제인데, 이게 제대로 짠게 맞는지 확인차 오랜만에 들어가서 돌려봤더니 다행히 '맞았습니다!!' 가 떴다. 이 문제를 풀기 위한 나머지 코드도 아래에 써둔다.
(나는 가끔가다 0-1배낭 문제에서 이런 걱정을 하곤한다. 점화식으로 dp 테이블을 채워나가던중 중간단계쯤에서 어떤 아이템이 등장하고 그 아이템의 무게는 이전 아이템들에 비해 정말 가볍고 가치는 엄청나다. 그런데 그 가벼운 무게를 담을 수 없을 정도로 가방의 남아있는 용량이 없다. 그래서 지금까지는 최적의 해를 구해왔지만 이제는 최적을 구할 수 없게 될 수도 있지 않을까? ==>>0-1 배낭문제의 점화식의 특성을 제대로 이해하지 못해서 생기는 걱정이다. 점화식을 보면 해당 아이템을 담았을시에 그 무게를 뺀 경우의 최적해를 부분해로 가져오고 있다(Vi +A[i-1][w-wi]). 이 경우를 물건을 넣지않았을때의 최적의 경우(A[i-1, w])와 비교하고 있는 것이다.)
wt = []
val = []
N, K = map(int, sys.stdin.readline().strip().split())
for i in range(N):
w, v = map(int, sys.stdin.readline().strip().split())
wt.append(w)
val.append(v)
print(knapsack(K, wt, val, N))
메모: map 함수는 2번째 인자의 값에다가 일괄적으로 1번째 인자에 해당하는 함수를 적용시켜주는 함수다. 알고리즘 문제를 많이 풀어보지 않아서 잘 몰랐는데, 보통 이런 식으로 값을 많이 받는 모양이더라. 입력받을 땐 문자열인데 써먹을 땐 숫자로 써야 하니까 일괄적으로 int() 를 먹여서 타입 캐스팅을 해주는 것이다.
from sys import stdin
def knapsack(n, totalW, wt, val):
k=[[0]*(totalW+1) for _ in range(n+1)]
for i in range(n+1):
for w in range(totalW+1):
if(i==0 or w==0):
k[i][w]=0
elif(wt[i]<=w):
k[i][w]=max(val[i]+k[i-1][w-wt[i]], k[i-1][w])
else:
k[i][w]=k[i-1][w]
return k[n][totalW]
def main():
num=int(stdin.readline())
for _ in range(num):
val=[0]
wt=[0]
totalW, n=map(int, stdin.readline().split())
data=list(map(int, stdin.readline().split()))
for v,w in zip(data[0::2],data[1::2]):
val.append(v)
wt.append(w)
print(knapsack(n, totalW, wt, val))
main()import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void knapsack(int n, int totalW, int[]weight, int[]value){
int[][]dp=new int[n+1][totalW+1];
for(int i=0;i<n+1;i++){
for(int w=0;w<totalW+1;w++){
if(i==0 || w==0)
continue;
else if(weight[i]<=w)
dp[i][w]=Math.max(value[i]+dp[i-1][w-weight[i]], dp[i-1][w]);
else
dp[i][w]=dp[i-1][w];
}
}
System.out.println(dp[n][totalW]);
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int totalW = Integer.parseInt(st.nextToken());
int[] weight = new int[n + 1];
int[] value = new int[n + 1];
for (int i = 1; i <= n; i++) {
st=new StringTokenizer(br.readLine());
weight[i]=Integer.parseInt(st.nextToken());
value[i]=Integer.parseInt(st.nextToken());
}
knapsack(n, totalW, weight, value);
}
}
'알고리즘 > DP(Dynamic programming, 동적프로그래밍)' 카테고리의 다른 글
| [백준] 2293 동전1 (0) | 2023.05.31 |
|---|---|
| [백준] 11066번: 파일 합치기 (0) | 2023.05.20 |
| [백준] 9251번 : LCS(Longest Common Subsequence) (0) | 2023.05.19 |
| DP 기본문제인 막대기 자르기(백준에 없는문제) (0) | 2023.02.14 |
| 동적프로그래밍의 개념과 기본 개념을 잡아주는 피보나치 문제 (0) | 2023.02.14 |


