백준(BOJ) 9461: 파도반 수열

 

출처: https://www.acmicpc.net/problem/9461

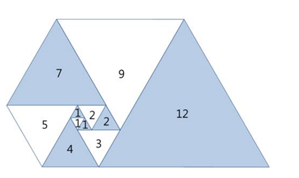
최적해를 어떻게 하면 부분해를 이용해서 점화식으로 세울수 있을지를 고민해야 한다.

만약 수열이라는 것이 주워지면 문제가 다 풀린것이나 마찬가지다.  최적해와 부분해의 관계를 가진 점화식을 세우기가 한결수월해 진다. 그리고 주워진 그림과 그 수열을 함께 가지고 생각한다면 점화식은 더 쉽게 얻어진다.

처음에는 예외가 존재하지만 나중으로가면 결국은 최적해는 이전의 두개의 삼각형의 변을 합한 것이 된다는 것을 쉽게 찾을 수 있다. 
즉 n=6이상에서 점화식은 An=An-1+An-5가 된다.

 

마지막으로 주의할 것은 자료형이 커버할 수 있는 범위이다. n=100일때 그답은 int 형으로 커버할수 없어 틀렸다고 나왔다.(Overflow나 다른 에러가 아닌 단순히 틀렸다고 나와 어쩔수 없이 구글링하여 문제를 일일히 찾아야 했다.) dp배열의 자료형을 int가 아닌 long으로 해주면 해결된다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.lang.reflect.Array;
import java.util.Arrays;

public class Testing3{
    public static void solution(int n){
        if(n<=3){
            System.out.println(1);
            return;
        }
        else if(n<=5){
            System.out.println(2);
            return;
        }
        long[]dp=new long[n+1];
        Arrays.fill(dp, 1,4, 1);
        Arrays.fill(dp, 4,6,2);
        for(int i=6;i<=n;++i)
            dp[i]=dp[i-1]+dp[i-5];

        System.out.println(dp[n]);
    }
    public static void main(String[] args)throws Exception{
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        int T=Integer.parseInt(br.readLine());
        for(int t=0;t<T;t++){
            int n=Integer.parseInt(br.readLine());
            solution(n);
        }
    }
}